DNN Training Stages Understanding
Recent works show that DNN training undergoes different stages, each stage shows different effects given a hyper-parameter setting and therefore entails detailed explaination. Below I aims to analyze and share the deep understanding of DNN training, especially from the following three perspectives:
- On the optimization and generalization perspective
- On the frequency domain perspective
- What happens during the early phase of DNN training
On the Optimization and Generalization Perspective
The connection between optimization and generalization of deep neural networks (DNN) is not fully understood. For instance, using a large initial learning rate often improves generalization, which can come at the expense of the initial training loss reduction. In this context four works targeting understanding the connection between optimization and generalization are discussed below.
The Two Regimes of Deep Network Training: Learning rate schedule has a major impact on the performance of deep learning models. Instead of heuristical choice, This paper aims to understand the effects of different learning rate schedules and therefore develop a appropriate way to select. Specifically, two regimes are discussed:
1. Large-step regime: the highest LR w/o loss divergence 2. Small-step regime: the highest LR when loss consistently decrease There is no sharp boundary between them. But the two regimes show large difference in both optimization and generalization effects. For optimization as visualized in Fig. 1, large-step regime are less effective than small-step couterpart, i.e., perform worse loss convergence, and show completely opposite reaction to the momentum, which is a balance item with $\mu$ as coefficient added to the gradient: $g^{t+1} = \mu \cdot g^t + \nabla f$. Specifically, adding momentum makes worse optimization effect for large-step regime while favors small-step regime, this phenomenon accounts for two reasons: 1) small-step regime are easier to be trapped into small convex valley in loss surface; 2) momentum accelerates the optimization for convex function and therefore align with the small-step regime while counter the large-step regime.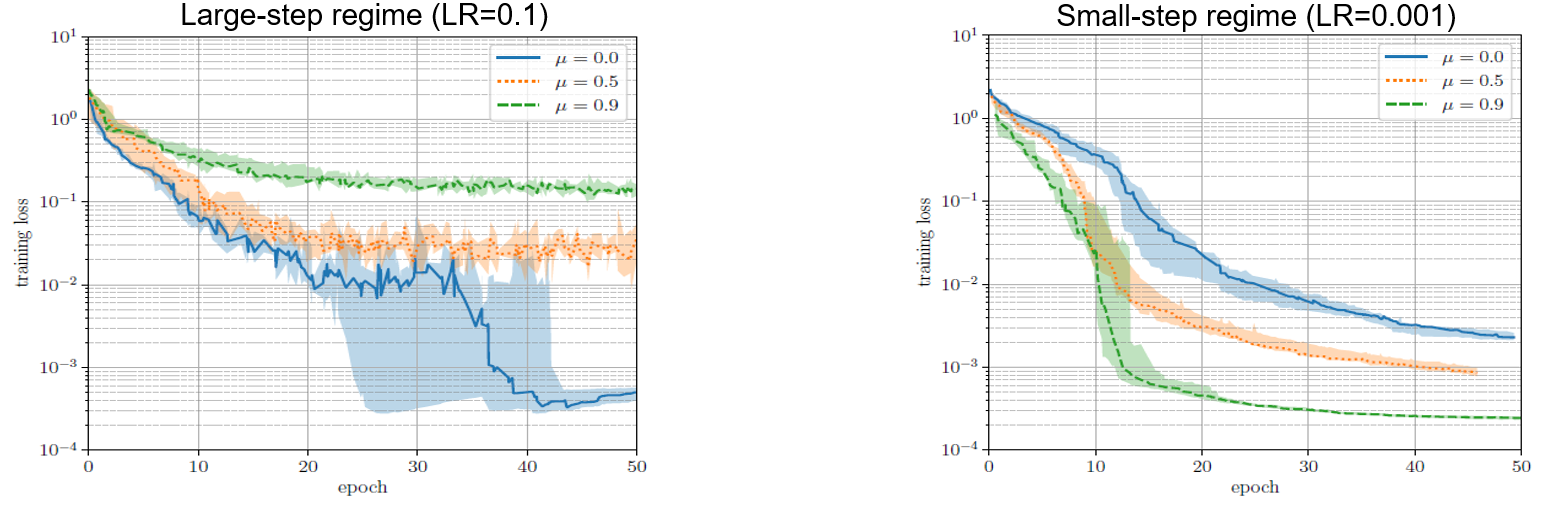
Fig.1 - Loss trajectory under the two regimes and different momentum values.
On the other hand, the two regimes inherit the same reaction to momentum from the generalization perspective.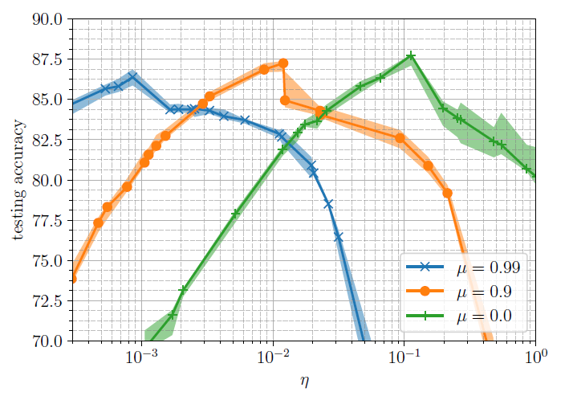
Fig.2 - Test accuracy under the different learning rates $\eta$ and momentums $\mu$.
Build upon the aforementioned two regimes, this paper proposes a new training scheme, including two stages: 1) use large-step regime targeting good generalization; 2) use small-step regime coupled with large momentum targeting good optimization. Also, they show the ablation study of the transition epoch from the first stage to the second stage, benchmarking on the referenced heuristical three-step learning rate schedule.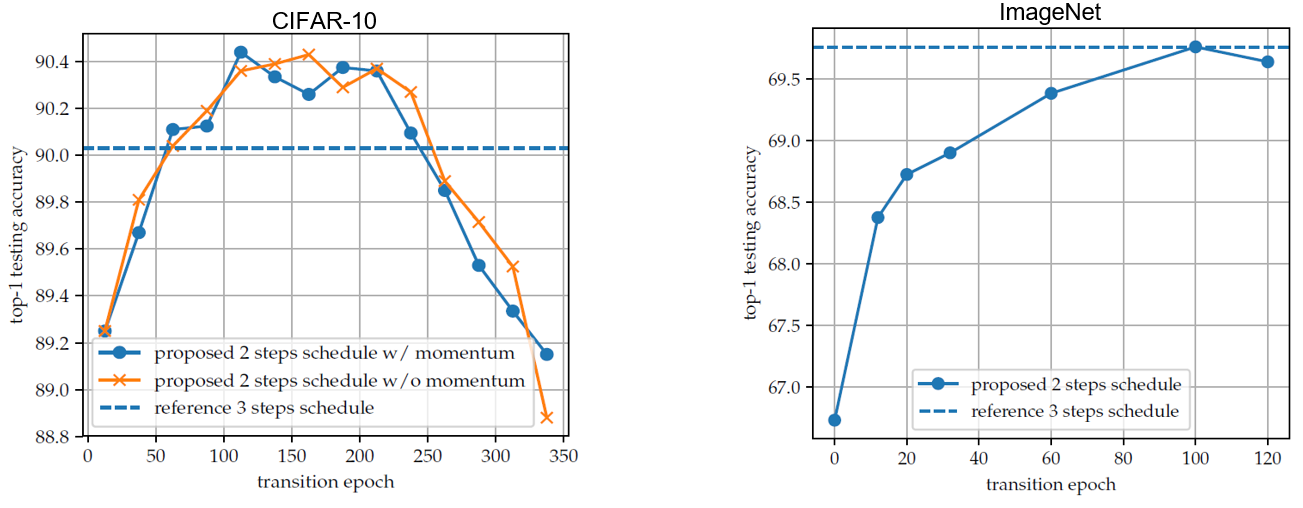
Fig.3 - Comparison between proposed schedule and the referenced classic three-step learning rate schedule. Towards Explaining the Regularization Effect of Initial Large Learning Rate in Training Neural Networks: This paper shares the same motivation with two regime one, toward explaining the effectiveness of initial large learning rate and annealing scheme theoretically. The unique contribution is that it gives the concrete proof for two-layer fully connected networks case.
Stiffness: A New Perspective on Generalization in Neural Networks: This paper investigates neural network training and generalization using the concept of stiffness. Specifically, it measures how stiff is a network by looking at how a small gradient step on one example affects the loss on another example. Given data pair $(X, y)$, suppose the corresponding loss gradient can be represented by $\vec{g} = \nabla \mathcal{L} (f(X), y)$, then we can discuss the mutual influence caused by two independent data pairs, as shown in Fig. 4.
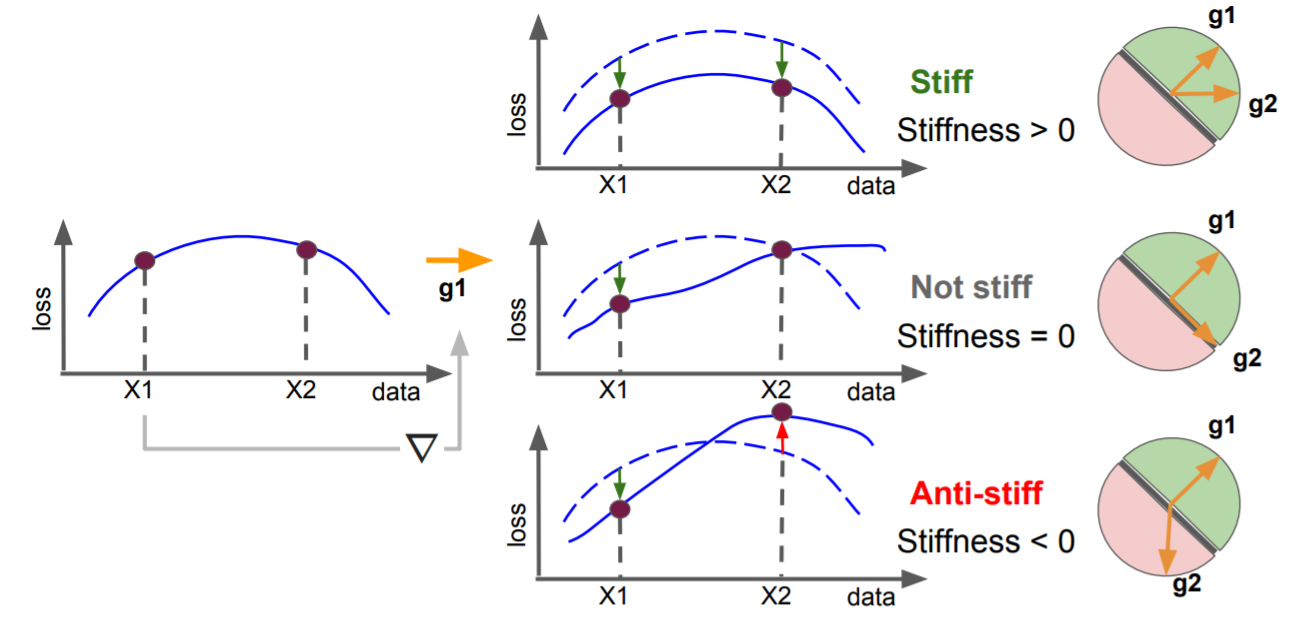
Fig.4 - A diagram illustrating the concept of stiffness. It can be viewed as the change in loss in an input induced by application of a gradient update based on another input. This is equivalent to the gradient alignment between gradients taken at the two inputs.
and then formulates the discrete (sign) or continuous (cos) stiffness metrics:$S_{sign/cos}((X_1, y_1); (X_2, y_2); f) = \mathbb{E}[\text{sign/cos}(\vec{g_1} \cdot \vec{g_2})]$Based on the proposed generalization metric, they visualize the change of stiffness of two data samples from the same/different classes, and find that the stiffness increase gradually during training, indicating the better and better generalization capability of network. Moreover, they evaluate the stiffness between data samples from training dataset and validation dataset, and find that the proposed metric can identify whether the network training is overfitting from only the training dataset. In particular, as illustrated in Fig. 5, when overfitting occurs, the stiffness measured from both training dataset (train-train) and between training and validation dataset (train-val) regress to zero! Which means we know when the network is overfitting without needs to validate, and demonstrates it is a good metric for quantify generalization.
Fig.5 - The evolution of training and validation loss (left panel), within-class stiffness (central panel) and between-classes stiffness (right panel) during training. The onset of over-fitting is marked in orange. The Break-Even Point on Optimization Trajectories of Deep Neural Networks: This paper investigates how the hyperparameters of SGD used in the early phase of training affect the rest of the optimization trajectory. Before talking about the concrete analysis, we need to keep in mind two concepts:
1. Spectrum of Hessian ($\lambda_H^1$): measure the local curvature of loss surface 2. Spectrum of Covariance of gradient ($\lambda_K^1$): measure the variance of gradient The first concept is the break-even point. Instead understanding it from mathematical equations, here I show the intuitively explaination: Assume the spectrum norm of Hessian is monotonically along the optimization trajectory, gradient descent reaches a point in the early phase of training at which it oscillates along the most curved direction of the loss surface, we call this point the break-even point. Specifically, the break-even point is where the spectrum norm of Hessian or Covariance of gradient saturates. Before that point, the spectrum norm will increase monotonically; after that point, the spectrum norm keep the value, meaning that optimization enter the convex-like hall in loss surface thereafter and the trajectory oscillates along the most curved direction. Also, the break-even point comes at the very early stage of network training. Fig. 6 demonstrates the assumption (the spectrum norm will increase monotonically) holds when training simple CNN on CIFAR-10 under two different learning rate setting. It also indicates that the saturate values are different if using different hyper-parameters.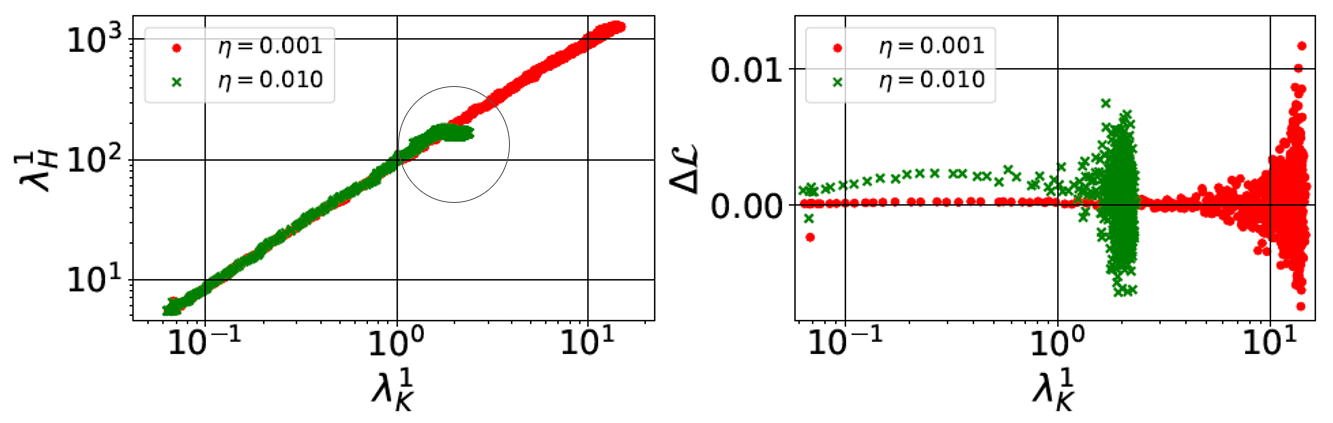 Then, to probe how the hyper-parameters of SGD used in the early phase of training matter, one can visualize the optimization trajectories under different hyper-parameter settings in Fig. 7 (i.e., large/small learning rate here). At the beginning, the two settings are optimized from the same initialization and therefore share the same trajectory. After a while, their trajectories diverge towards different directions until reaching the break-even points. While large learning rate reaches smaller $\lambda_K^1$ than its counterpart and shows good generalization thereafter.
Then, to probe how the hyper-parameters of SGD used in the early phase of training matter, one can visualize the optimization trajectories under different hyper-parameter settings in Fig. 7 (i.e., large/small learning rate here). At the beginning, the two settings are optimized from the same initialization and therefore share the same trajectory. After a while, their trajectories diverge towards different directions until reaching the break-even points. While large learning rate reaches smaller $\lambda_K^1$ than its counterpart and shows good generalization thereafter.Fig.6 - The spectral norm of $H$($\lambda_H^1$, left) and $\Delta L$ (difference in the training loss computed between two consecutive steps, right) versus $\lambda_K^1$ at different training iterations. 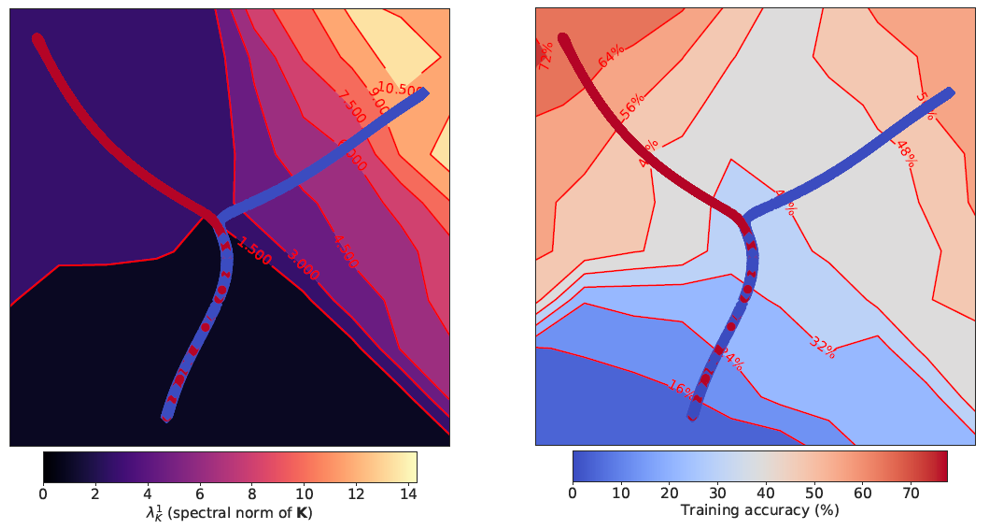
Fig.7 - Visualization of the early part of the training trajectories on CIFAR-10 before reaching 65% training accuracy (break-even point). Red line: LR=0.01; Blue line: LR=0.001.
Based on the break-even points observation, this paper proposes two conjectures to investigate the effects of different hyper-parameters: 1. Along the SGD trajectory, the maximum attained values of $\lambda_H^1$ and $\lambda_K^1$ are smaller for a larger learning rate or a smaller batch size. 2. Along the SGD trajectory, the maximum attained values of $\lambda_H^* / \lambda_H^1$ and $\lambda_K^* / \lambda_K^1$ are larger for a larger learning rate or a smaller batch size.
Fig.8 - The optimization trajectories corresponding to higher learning rates ($\eta$) or lower batch sizes ($S$).
On the Frequency Domain Perspective
Understanding the training process of Deep Neural Networks (DNN) is a fundamental problem in the area of deep learning. Here is the papers analyzing DNN training from the frequency domain perspective. The concept of “frequency” is central to the understanding of below papers. In this context, the “frequency” means response frequency NOT image (or input) frequency as explained in the following.
Training Behavior of Deep Neural Network in Frequency Domain: This paper analyze the network training from the frequency perspective, aiming to claim the F-Principle: DNNs often fit target functions from low to high frequencies during the training process.
One of the difficulties of requency analysis for image classification is how to compute the high-dimensional Fourier transform given dataset $(x_k, y_k)$. They use the first principal component of inputs $x_k = x_k \cdot v_{PC}$. Then, Using Fourier transform, we can represent the dataset in frequency domain:$\mathcal{F}_{PC}[y](\gamma) = \frac{1}{n} \sum_{j=1}^{n-1} y_j \cdot exp(-2\pi i x_j \gamma)$Where $\gamma$ is the frequency index. Suppose network prediction is $T(x_k)$, then define the relative difference as:$\Delta_F(\gamma) = \frac{|\mathcal{F}_{PC}[y](\gamma) - \mathcal{F}_{PC}[T](\gamma)|}{|\mathcal{F}_{PC}[y](\gamma)|}$We can view the defined relative difference as frequency loss, measuring the similarity between the frequency of ground truth and predictions. This paper visualizes the changes of frequency loss at several selected frequency indexes during training, shown as Fig. 9.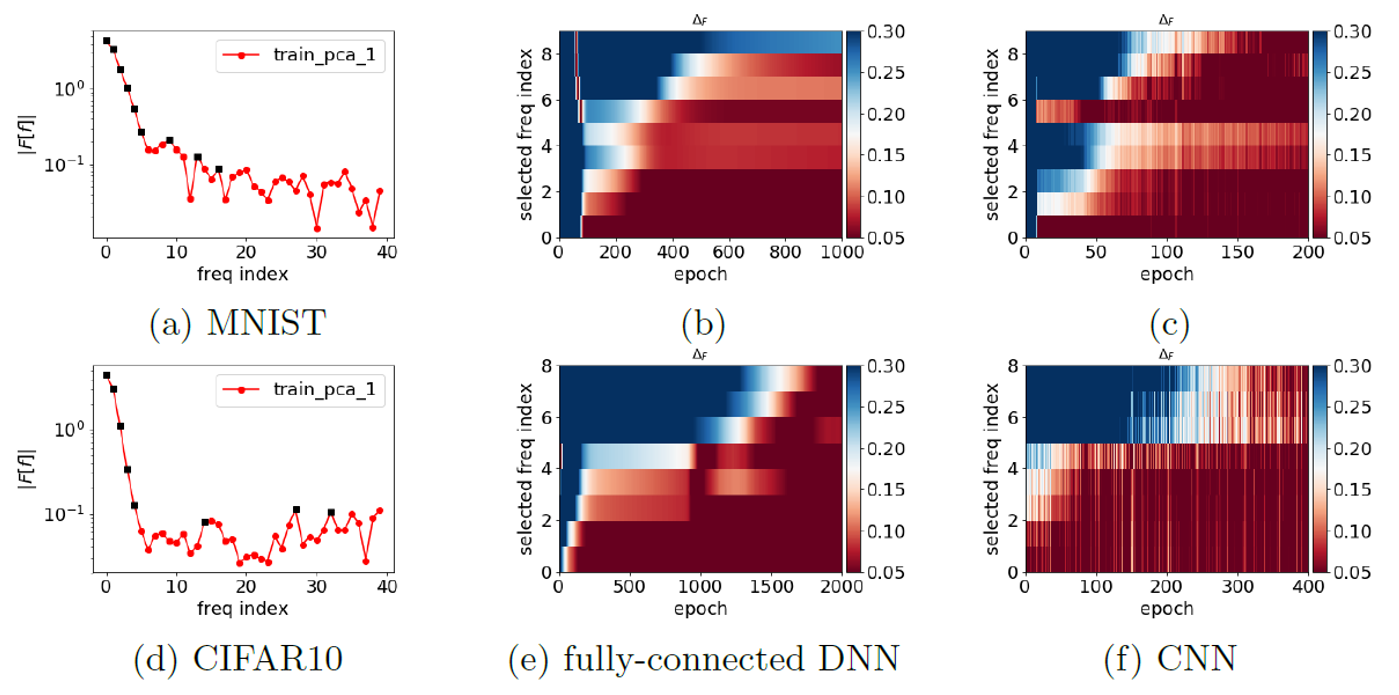
Fig.9 - Frequency analysis of DNN output function along the first principle component during the training. The training datasets for the first and the second row are from MNIST and CIFAR10, respectively. The neural networks for the second column and the third column are fully-connected DNN and CNN, respectively.
By examining the relative error of certain selected key frequency components (marked by black squares), one can clearly observe that DNN of both structures for both datasets tend to capture the training data in an order from low to high frequencies as stated by the F-Principle.On the Spectral Bias of Neural Networks: This paper shares the same motivation and claim with F-Principle.
What happens during the early phase of DNN training
Similar to humans and animals, deep artificial neural networks exhibit critical periods, which is exactly the early phase of training. A lot of phenomenons have been discovered during the early phase of network trianing. For example, sparse, trainable sub-networks emerge, gradient descent moves into a small subspace, and the network undergoes a critical period. Below two recent works are briefly introduced.
Critical Learning Periods in Deep Networks: Researchers have documented critical periods affecting a range of species and system, as a machine learning researcher, one is supposed to explore whether neural network training also experience such critical periods. If so, when is the critical period? This paper gives us the answer using deficit ablation study.
To explore whether critical periods exists in network trianing, this paper measures the test accuracy affected by the deficit as a function of the epoch $N$ at which the deficit is corrected. From Fig.10, we can readily observe the existence of a critical period: If the blur is not removed within the first 40-60 epochs, the final performance is severely decreased when compared to the baseline.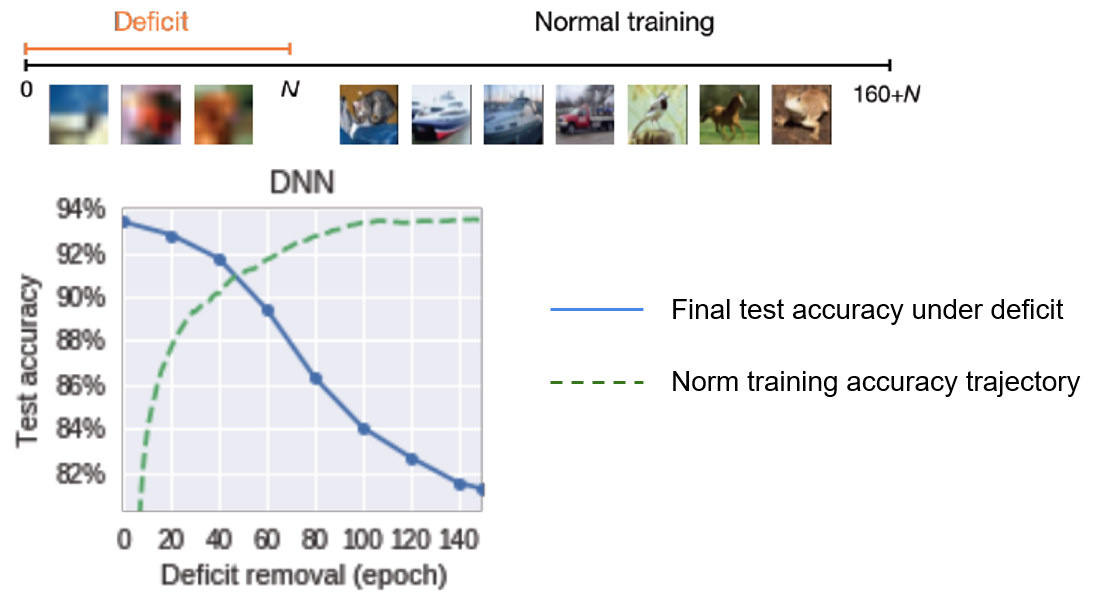
Fig.10 - Final test accuracy of a CNN trained with a cataract-like deficit as a function of transition epoch at which deficit is removed.
Further, to explore whether critical periods is early training phase, they conduct another ablation of deficit starting epoch. The decrease in the final performance can be used to measure the sensitivity to deficit, the most sensitive epochs corresponds to the early rapid training phase. Afterwards, the network is largely unaffected by the temporary deficit.
Fig.11 - The decrease of final performance of a CNN as a function of the onset of a short 40 epochs deficit. The Early Phase of Neural Network Training: Since early stage of trianing is critical, this paper investigates it further, aiming to provide a unified framework for understanding the changes that DNNs undergo during this early phase of training.
They first provide a detailed statistical summary of the changes in early training phase, taking ResNet-20 on CIFAR-10 as an example.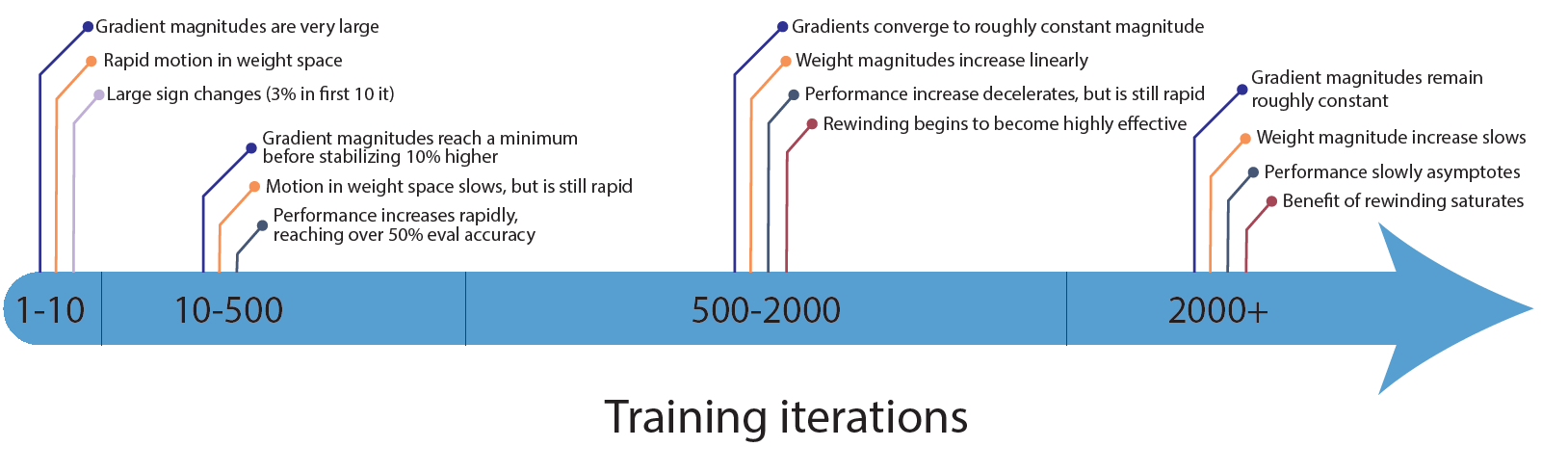
Fig.12 - Rough timeline of the early phase of training for ResNet-20 on CIFAR-10.
Among them, the most attractive pheonmenon is that during 500-2000 iterations (2-10 epochs; 1⁄80-1⁄16 training stages), rewinding starts to be highly effective. Build upon Lottery Ticket Hypothesis (LTH), something important happens during the early phase of training so that rewinding the network should go to these early phases instead of the initial phase. As demonstrated by Fig. 13, rewinding variants perform better than lottery initialization.
Fig.13 - Accuracy of IMP (Iterative Magnitude Pruning) when rewinding to various iterations of the early phase for ResNet-20 sub-networks as a function of sparsity level.
Then, they probe what is more important for the early phase of training: signs of the weights or magnitude of the weights? By conductin ablation studies of weight signs and weight magnitude from initialization or early phase, this paper finds that both signs and magnitude are important to handle highly sparse scenarios. Also, they probe whether the weight in early phase can be sampled from a distribution, by shuffling the weight globally or locally and then test their performance under highly sparse scenarios. They find that the weights do not show distributionality at all, thus the early phase of training is the only way to get good initialization in retraining phase so far.